In this post, I’ll show why people in the last U.S. election voted for Trump, which is the same as saying against Clinton because the fringe candidates hardly received any votes, relatively speaking.
The technique here handles one of the most vexing questions in black-box classifier and regression models: Which variables should you remove from a regression model to make it more accurate?
(This article is part of our scikit-learn Guide. Use the right-hand menu to navigate.)
How permutation importance works
Within the ELI5 scikit-learn Python framework, we’ll use the permutation importance method. Permutation importance works for many scikit-learn estimators. It shuffles the data and removes different input variables in order to see relative changes in calculating the training model. It also measures how much the outcome goes up or down given the input variable, thus calculating their impact on the results.
In other words, for linear regression, it first calculates, for example, the coefficients α, β, γ, …
y = αa + βb + γc + … + ωz + B
And then tests the model using cross entropy, or another technique, then calculating r2 score, F1, and accuracy. Finally, the model drops one of a, b, c, … and runs it again.
There are two downsides to this method:
- Other ML frameworks do not support this.
- Its output is an HTML object that can only be displayed using iPython (aka Jupyter).
Running Jupyter
Nothing can be easier that running Jupyter—it is easier to set up that Zeppelin, which itself requires little setup. Simply install Anaconda and then, on Mac, type jupyter notebook. It will open this URL in the browser http://localhost:8889/tree.
Clinton v. Trump
First, get your U.S. election data here. These summaries are for every county in every state in the U.S. The code we write is stored here.
We use the read_csv Pandas method to read the election data, taking only a few of the columns. You could add more columns to find what other variables correlate with the voter’s choice.
At the bottom is the complete code. Here we explain different sections. But first, here are the results in both HTML and text format.
So you can see the columns in the data frame by their index, here they are are:
Index(['Trump', 'age65plus', 'SEX255214', 'White', 'Black', 'Hispanic', 'Edu_highschool'], dtype='object')
Here are the relative weights.
| column name | Weight | Feature |
| age65plus | 0.5458 ± 0.0367 | x0 |
| Hispanic | 0.3746 ± 0.0348 | x4 |
| White | 0.2959 ± 0.0159 | x2 |
| SEX255214 | 0.0323 ± 0.0064 | x1 |
| Edu_highschool | 0.0272 ± 0.0038 | x5 |
| Black | 0.0207 ± 0.0023 | x3 |
The graphic is shown in the iPython notebook as follow:
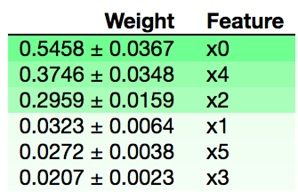
As you can see, the decision whether to vote for Trump is mainly by age, with voters 65 and over most closely correlated to the outcome. Surprisingly, gender does not matter much.
The code explained
In another blog, we explain how to perform a linear regression. The technique is the same here, except we use more than one independent variable, i.e., x.
We take as the independent variables xx, everything but Trump, which is the dependent variable, yy. A vote for Trump is a vote not for Hillary. So the output for the yy variable should the same, or similar, but it won’t be exactly the same as yy <> 1 – xx in the data.
We use the values properties of the dataframe to convert that to a NumPy array as that it what the fit method of LR requires.
xx = train[['White','Black','Hispanic','age65plus','Edu_highschool','SEX255214']].values yy = train[['Trump']].values
We do not need to reshape the arrays, as the dimensions fit the requirement that they can be paired up. xx has 3112 rows and 6 columns. yy is 3112 x 1.
xx.shape is (3112, 6) yy.shape is (3112, 1)
Next we run the fit method of linear_model. Then we print the coefficients:
Coefficients: [[ 0.51503519 -0.13783668 -0.44485146 0.00352575 -0.00985589 -0.00801731]]
Then comes the grand finale—running the fit method of PermutationImportance, followed by drawing the graph. This shuffles the input variables and runs linear regression multiple times, and then calculates which independent variables have the greatest impact on the calculation of the coefficients and thus y,
perm = PermutationImportance(reg, random_state=1).fit(xx, yy) eli5.show_weights(perm)
Here is the complete code.
import matplotlib.pyplot as plt
from sklearn import linear_model
import numpy as np
from sklearn.metrics import mean_squared_error, r2_score
import pandas as pd
import eli5
from eli5.sklearn import PermutationImportance
train = pd.read_csv('/Users/walkerrowe/Documents/keras/votes.csv',usecols=['Trump','White','Black','Hispanic','age65plus','Edu_highschool','SEX255214'])
xx = train[['White','Black','Hispanic','age65plus','Edu_highschool','SEX255214']].values
yy = train[['Trump']].values
reg = linear_model.LinearRegression()
model=reg.fit(xx,yy)
print('Coefficients: \n', reg.coef_)
perm = PermutationImportance(reg, random_state=1).fit(xx, yy)
eli5.show_weights(perm)
