So, you’ve built a machine learning model. Great. You give it your inputs and it gives you an output. Sometimes the output is right and sometimes it is wrong. You know the model is predicting at about an 86% accuracy because the predictions on your training test said so.
But, 86% is not a good enough accuracy metric. With it, you only uncover half the story. Sometimes, it may give you the wrong impression altogether. Precision, recall, and a confusion matrix…now that’s safer. Let’s take a look.
What is a confusion matrix?
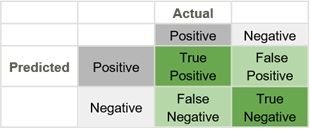
Both precision and recall can be interpreted from the confusion matrix, so we start there. The confusion matrix is used to display how well a model made its predictions.
Binary classification
Let’s look at an example: A model is used to predict whether a driver will turn left or right at a light. This is a binary classification. It can work on any prediction task that makes a yes or no, or true or false, distinction.
The purpose of the confusion matrix is to show how…well, how confused the model is. To do so, we introduce two concepts: false positives and false negatives.
- If the model is to predict the positive (left) and the negative (right), then the false positive is predicting left when the actual direction is right.
- A false negative works the opposite way; the model predicts right, but the actual result is left.
Using a confusion matrix, these numbers can be shown on the chart as such:
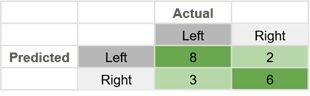
In this confusion matrix, there are 19 total predictions made. 14 are correct and 5 are wrong.
- The False Negative cell, number 3, means that the model predicted a negative, and the actual was a positive.
- The False Positive cell, number 2, means that the model predicted a positive, but the actual was a negative.
The false positive means little to the direction a person chooses at this point. But, if you added some stakes to the choice, like choosing right led to a huge reward, and falsely choosing it meant certain death, then now there are stakes on the decision, and a false negative could be very costly. We would only want the model to make the decision if it were 100% certain that was the choice to make.
Cost/benefit of confusion
Weighing the cost and benefits of choices gives meaning to the confusion matrix. The Instagram algorithm needs to put a nudity filter on all the pictures people post, so a nude photo classifier is created to detect any nudity. If a nude picture gets posted and makes it past the filter, that could be very costly to Instagram. So, they are going to try to classify more things than necessary to filter every nude photo because the cost of failure is so high.
Non-binary classification
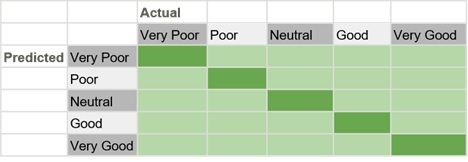
Finally, confusion matrices do not apply only to a binary classifier. They can be used on any number of categories a model needs, and the same rules of analysis apply. For instance, a matrix can be made to classify people’s assessments of the Democratic National Debate:
- Very poor
- Poor
- Neutral
- Good
- Very good
All the predictions the model makes can get placed in a confusion matrix:
Precision in Confusion Matrix
Precision is the ratio of true positives to the total of the true positives and false positives. Precision looks to see how much junk positives got thrown in the mix. If there are no bad positives (those FPs), then the model had 100% precision. The more FPs that get into the mix, the uglier that precision is going to look.
To calculate a model’s precision, we need the positive and negative numbers from the confusion matrix.
Precision = TP/(TP + FP)
Recall in Confusion Matrix
Recall goes another route. Instead of looking at the number of false positives the model predicted, recall looks at the number of false negatives that were thrown into the prediction mix.
Recall = TP/(TP + FN)
The recall rate is penalized whenever a false negative is predicted. Because the penalties in precision and recall are opposites, so too are the equations themselves. Precision and recall are the yin and yang of assessing the confusion matrix.
Recall vs precision: one or the other?
As seen before, when understanding the confusion matrix, sometimes a model might want to allow for more false negatives to slip by. That would result in higher precision because false negatives don’t penalize the recall equation. (There, they’re a virtue.)
Sometimes a model might want to allow for more false positives to slip by, resulting in higher recall, because false positives are not accounted for.
Generally, a model cannot have both high recall and high precision. There is a cost associated with getting higher points in recall or precision. A model may have an equilibrium point where the two, precision and recall, are the same, but when the model gets tweaked to squeeze a few more percentage points on its precision, that will likely lower the recall rate.
Additional resources
Get more on machine learning with these resources:
- BMC Machine Learning & Big Data Blog
- Machine Learning: Hype vs Reality
- Interpretability vs Explainability: The Black Box of Machine Learning
- Machine Learning with TensorFlow & Keras, a hands-on Guide
- This great colab notebook demonstrates, in code, confusion matrices, precision, and recall
For a mathematical understanding of precision and recall, watch this video:
For a more humorous look at confusion matrices:







